| We labeled that as our 'initial' group of findings because we wanted something more. Those were all great examples of what Dr. Wiggins was looking for, but they were just examples. We felt like we should be able to generalize those examples into an umbrella statement about the Pythagorean Theorem. I gave the kids a hint that we'd find that generalization when they could determine which two of the photos were telling a slightly different story than the other eight. It wasn't necessarily a search for those that look the coolest or scariest (meaning the diagrams ... not the kids). When they managed an answer to that, we'd be ready for our last upload.
When looking for the two photos that told a different story, kids didn't find it immediately apparent. As a result, we
started grouping photos that looked to be telling the same story. For example, the equilateral triangles
and the regular pentagons were just sub-cases of the regular n-gons. Since those three went together, they must
have been a part of the eight that were not as interesting as the mystery two. Furthermore, the dodecahedron proof
seemed to fit with the pentagon proof; the semicircles could be
classified as an n-gon with regular sides. As a matter of fact, when we moved them around, ...
... the idea of 'regular' came up a lot. When we separated out those that were of regular figures, we were left with just two.
While these trios of figures weren't regular, they were similar (or proportional) to each other.
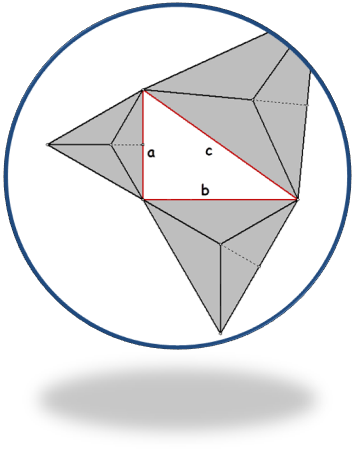
Would the Pythagorean relationship hold for any group of proportional figures that are sized
according to a Pythagorean triple? To find out, we decided to analyze an incredibly irregular figure.
|

|